Imagem de fundo

Dentro de circuitos digitais, temos alguns componentes que são importantes na construçã...

1
Q3366106
Teclas de Atalhos
Compartilhar
Ano: 2024
Banca: Associação Catarinense das Fundações Educacionais - ACAFE
Prova: ACAFE - CELESC - Técnico Industrial - Área Eletrônica - 2024

Dentro de circuitos digitais, temos alguns componentes que são importantes na construção do caminho de dados e, como exemplo, podemos citar os circuitos somador e subtrator. Uma forma de economizar na construção dos circuitos citados é por meio da combinação dos dois circuitos, como mostrado na figura.



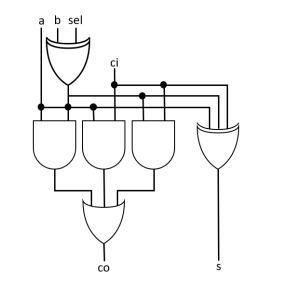
Sabendo que “sel” permite selecionar soma ou subtração, “a” e “b” são os operandos, “ci” é carry-in, “co” é o carry-out e “s” é a saída, as equações booleanas CORRETAS, que definem o somador/subtrator completo, são:

A

s = a ⊕ (b ⊕ sel) ⊕ ci e co = a(b ⊕ sel) + aci + (b ⊕ sel)ci.

B

s = a ⊕ (b ⊕ sel)ci e co = a(b ⊕ sel) + a + ci + (b ⊕ sel)ci.

C

s = a ⊕ (b ⊕ sel) ⊕ (ci ⊕ sel) e co = a(b ⊕ sel) + a(ci ⊕ sel) + (b ⊕ sel)ci.

D

s = a ⊕ (b ⊕ ci) ⊕ sel e co = a(b ⊕ sel) + a(ci ⊕ sel) + (b ⊕ sel)ci.

E

s = sel ⊕ (a ⊕ sel) ⊕ b e co = a(b ⊕ sel) + aci + (b ⊕ sel)ci.